Rasiowa–Sikorski lemma

In axiomatic set theory, the Rasiowa–Sikorski lemma (named after Roman Sikorski and Helena Rasiowa) is one of the most fundamental facts used in the technique of forcing. In the area of forcing, a subset D of a forcing notion (P, ≤) is called dense in P if for any p ∈ P there is d ∈ D with d ≤ p. A filter F in P is called D-generic if

F ∩ E ≠ ∅ for all E ∈ D.

Now we can state the Rasiowa–Sikorski lemma:

Let (P, ≤) be a poset and p ∈ P. If D is a countable family of dense subsets of P then there exists a D-generic filter F in P such that p ∈ F.

Proof of the Rasiowa–Sikorski lemma

The proof runs as follows: since D is countable, one can enumerate the dense subsets of P as D₁, D₂, …. By assumption, there exists p ∈ P. Then by density, there exists p₁ ≤ p with p₁ ∈ D₁. Repeating, one gets … ≤ p₂ ≤ p₁ ≤ p with p_i ∈ D_i. Then G = { q ∈ P: ∃ i, q ≥ p_i} is a D-generic filter.

The Rasiowa–Sikorski lemma can be viewed as a weaker form of an equivalent to Martin's axiom. More specifically, it is equivalent to MA().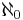

Examples

• For (P, ≥) = (Func(X, Y), ⊂), the poset of partial functions from X to Y, define D_x = {s ∈ P: x ∈ dom(s)}. If X is countable, the Rasiowa–Sikorski lemma yields a {D_x: x ∈ X}-generic filter F and thus a function ∪ F: X → Y.
• If we adhere to the notation used in dealing with D-generic filters, {H ∪ G₀: P_ijP_t} forms an H-generic filter.
• If D is uncountable, but of cardinality strictly smaller than 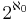and the poset has the countable chain condition, we can instead use Martin's axiom.

See also

• generic filter
• Martin's axiom

References

• Set Theory for the Working Mathematician. Ciesielski, Krzysztof. Cambridge University Press, 1997. ISBN 0-521-59465-0
• Kunen, Kenneth (1980). Set Theory: An Introduction to Independence Proofs. North-Holland. ISBN 0-444-85401-0. 

External links

• Tim Chow's newsgroup article Forcing for dummies is a good introduction to the concepts and ideas behind forcing; it covers the main ideas, omitting technical details